MDL test case: Chromo shadow family

.

For more information about this family see Rein Aaslands Chromo Domain WWW page. and
The chromo shadow domain, a second chromo domain in Heterchromatin-binding protein 1, HP1.
Rein Aasland and A. Francis Stewart.
Nucleic Acids Research 23(16): 3168-3173 (1995)

Old results

Sequences included in the analysis:

  1. Sequence segments included in Aasland and Stewart's NJ tree.
  2. Bigger set.

NJ tree generated by using Clustal W(calculation) and Phylip (drawing).

The alignment that was used to generate tree, made by Clustal W.

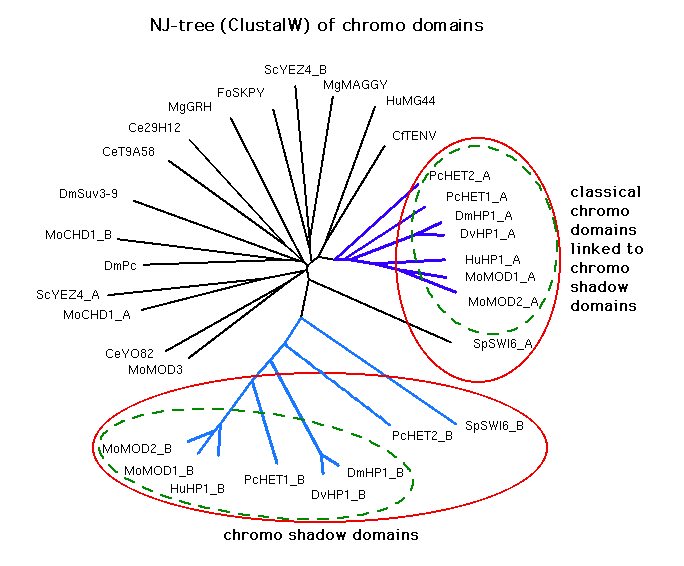
Aasland and Stewart's NJ tree showing an estimate of their evolutionary relationship:

New trees:

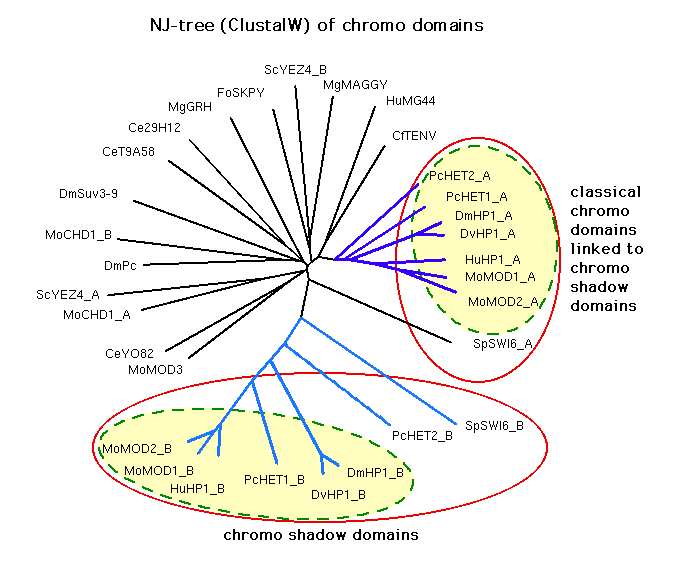
Results from running Pratt with the MDL set cover algorithm

First Pratt was run on the complete set of sequences, using different K-values (minimum number of sequences to match a pattern). The pattern having the maximum C-value was chosen, and the sequences matching this pattern was removed from the set of sequences. The remaining set of sequences were analysed in the same way. This was repeated until the number of sequences left was less than 4. The resulting set of patterns covers the set of sequences in a close-to-optimal way according to the Minimum Length Description (MDL) principle. Different tests were done using different scoring schemes:

  1. Using the equation given in the paper, C(p,l)=I(p)-c0-(c1 |p| + c2 #X(p) +c3)/l, and parameters (c0,c1,c2,c3)= (10,10,3,10).

  2. Using the equation C(p,l)=I(p)-(c1 |p| + c2 #X(p) +c3)/l (identical to the one above except that c0 is not included). Different values for the parameters were used; (c1,c2,c3)=
    1. (8,3,50)
    2. (8,3,100)
    3. (8,3,150)
    4. (8,3,300)
    5. (3,2,50)
    6. (10,2,50)
    7. (10,2,100)
    8. (12,2,100)
    9. (15,2,50)

Example:
For the Z=5.0 example, we get sets of sizes: 7, 7, 12, and 8 (standard algorithm) and 7, 7, 11, 8, and 1 (complete). Examples of sequences of K-values used by the standard algorithm when analysing sets of size N sequences:
Sequence of K-values used for N=34: 34, 29, 24, 20, 16, 13, 11, 9, 8, 7, 6, 5, 4.
Sequence of K-values used for N=27: 27, 24 20, 16, 13, 11, 9, 8, 7, 6, 5, 4.
Sequence of K-values used for N=18: 18, 16, 13, 11, 9, 8 7, 6, 5, 4.
Sequence of K-values used for N=13: 13, 11, 9, 8 7, 6, 5, 4.

We see that most of the chromo shadow domains are very seldom put in the same group as any of the other sequences, and less often so than some of the classical chromo domains liked to chromo shadow domains. The chromo shadow domains also seem to constitute a more separate subtree than the classical chromo domains liked to chromo shadow domains.

Page compiled by: Inge Jonassen.

MDL test cases,