Example: Heatflow in one dimension
This is an example of
efficient prototyping of recurrences
applied to a simple partial differential equation.
The 1-dimensional heat flow equation describes the heat distribution u(x,t) in
a one-dimensional object along the x-axis at time t. Alpha is a physical constant describing the heat transfusion properties of the object.
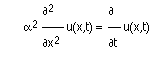
To turn this into a recurrence relation we may use the finite difference
method, achieving
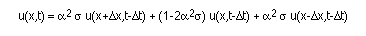
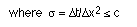
The c is a numerical constant, relating the size of the time steps to the size of the
object grid. If the quotient is larger than c we loose numerical stability of the
method. Abstracting the stencil, we may express the recurrence
as a recursive program with the explicit stencil
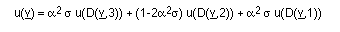
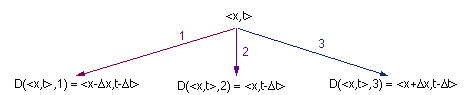
The kernel of the program actually compiled follows, where we take into account
the boundary conditions (a constant temperature given at the start of the
computation)
h(n) =
if(right_boundary(n) or left_boundary(n)
then h(d(n,2))
else
s*h(d(n,1))
+ (1-2*s)*h(d(n,2))
+ s*h((d(n,3)
The actual computation is defined on an integer grid x int * t int
rather than in real coordinates. The opposite of the stencil becomes
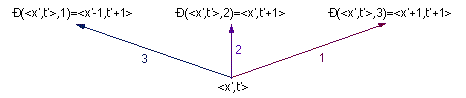
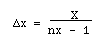
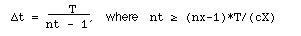
where nx is the number of nodes in the discretisation of the object (with
length X) in the x-direction, nt is the number of nodes in the
discretisation of the simulated time (with length T). The number of time
nodes nt is related to the number of space node nx by the given formula.
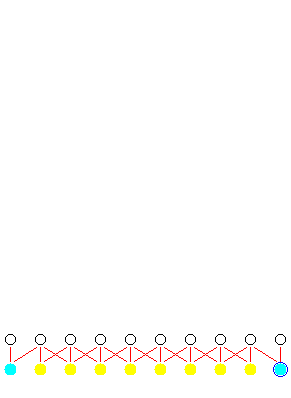
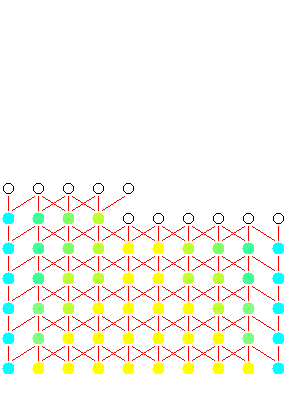
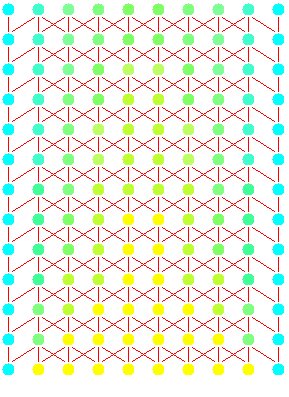
Heatflow computation
The following is a sequence of snapshots of the actual computation generated
by the compiler.
The temperature has been encoded using colours. Initially the rod is hot (yellow),
with a constant cold temperature (blue) being applied at the ends. During time
the rod cools off from the edges (hues of green).
After sending initial values:
While computing:
Complete computation:
You can watch an animated demo of this if your
browser supports Java.
In the parallel case all nodes at the same timestep would be computed
simultaneously. An animated demo
of this has also been prepared as a Java applet.
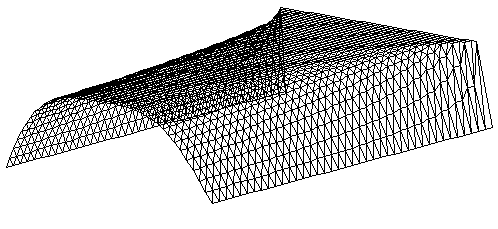
Heatflow result
Below the temperature of the object has been plotted against time in
a wireframe image. You may view this as a
rotatable image written in Java.
This was an example of efficient prototyping of recurrences.
© 1997 Magne Haveraaen, University of Bergen, Norway.
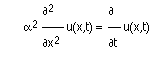
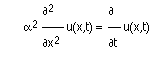
![]()
![]()
![]()
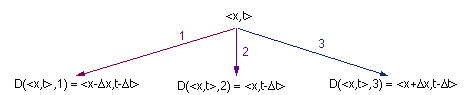
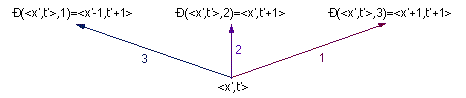
![]()
![]()