Example: Two Butterfly Algorithms
This is an example of
efficient prototyping of recurrences
used on algorithms that exhibit a butterfly dependency pattern.
The butterfly is a graph with a regular pattern, but the pattern
depends on the position in and size of the butterfly. A height 4
butterfly looks like
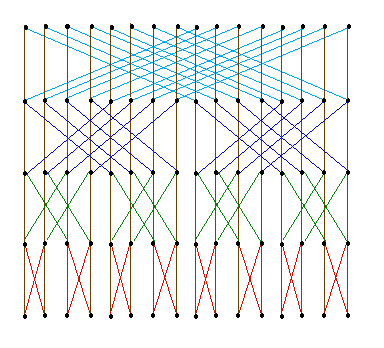
A butterfly of height h will have h+1 rows (indexed
0 through h) and 2^h
columns (indexed 0 through 2^h-1). A node is identified
by index pairs in
the the row-column order, thus for a height h butterfly we will be using
indices in the range <0,0>; through <h,2^h-1>. A precise
definition of the butterfly is given by the following:
- A height 0 butterfly has 1 node indexed by <0,0>
- A height h, for h>0, butterfly is composed horizontally from two
height h-1 butterflies placed side by side, such that 2^(h-1) is
added to the column numbers of the rightmost subbutterfly. Then a
new top row with indices <h,0> through <h,2^h-1> is added. A
node p=<i,j>; in the top row is connected by a vertical arc to
the node <i-1,j> (a top node in one of the butterflies of
height h-1) and by a diagonal arc to the node
<i-1,complementbit(j,i-1)>. That is, each new node is connect to the
node right under it (a topmost node in one of the subbutterflies)
and diagonally to the corresponding top node of the other
subbutterfly.
Replicated sum
Assume that the 0'th row of the butterfly has been assigned some number.
The replicated sum will add these numbers together, so that each node at
the top will receive a copy of the sum. The intermediate nodes will
contain various subsums.
sum(p) = sum(D(p,1)) + sum(D(p,2))
Fast Fourier Transform
The fast Fourier transform, the FFT, is a standard algorithm which
utilises the butterfly structure fully. The inputs are placed on the
bottom row, and the outputs appear on the top row.
fft(p) = fft(D(p,1)) + exp(a*row(p)/(2**col(p)))*fft(D(p,2))
The total execution time is n log n, where n=2^h is the number of input
nodes, as expected of the FFT algorithm.
This was an example of efficient prototyping of recurrences.
© 1997 Magne Haveraaen, University of Bergen, Norway.

