Institutt for Informatikk
Universitetet i Bergen
INF 225 - Innføring i Programoversettelse - H07
Voluntary Exercise Set 2 (Groupmeeting 13.09.2007)
1. Clearly indicate whether each statement below is True or False, and justify your answer.
a.) The regular expression (ba | b) * describes the set of all strings from the alphabet{a, b} that do not contain two consecutive a's.
b.) The regular expression (a (a | b)* )+ describes the same language as a (a | b)*.
2. For each regular expression below, either indicate it that represents the same language as that accepted by the DFA below, or prove that it does not represent the same language. (An easy way to prove that it does accept the same language is to give either a string that is accepted by the DFA but not by the regular expression or a string that is accepted by the regular expression but is not accepted by the DFA.)

a.) a+b | b+a
b.) (a | b)*
c.) (aa*b | bb*a)(a | b)*
d.) a+ba* | a+bb* | b+ab* | b+aa*
e.) (a | b) (a* | b*) (b | a) (a | b)*
f.) (a+b | b+a)(a | b)*
3. Exercise 2.12 on page 92 of the text.
4. Use subset construction to convert the following NFA to an equivalent DFA. Assume the transitions without labels are e-transitions.
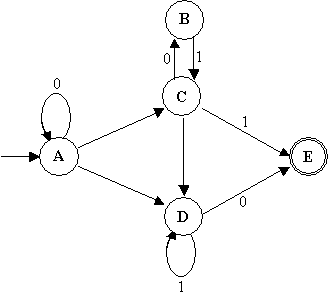
5. Exercise 2.16 on page 92 of the text.
6. Exercise 2.17 on page 93 of the text.
7. Exercise 2.22 on page 93 of the text.
8. Exercise 2.24 on page 93 of the text.