V.2 (Not a final version)

Uniformly Reflexive Structures

and URSA-minor

Uniformly reflexive structures (URS) are an axiomatic approach to computability. They were introduced in my 1963 doctoral dissertation at Columbia University. These pages provide an introduction to URS in general but the main thing we do here is introduce a simple functional language, URSA-minor, based on the URS concept, together with a calculator for writing and evaluating URSA-minor programs. The calculator is implemented in JavaScript and thus it provides a way to handle higher level functions within JavaScript.

The URS Concept

The original motivation was to axiomatize the idea of a Gödelization, such as those used in the theory of computability, but in a very general setting. In the theory of computability a Gödelization is essentially an enumeration of the (one argument) computable functions by natural numbers which is "effective" in the sense that there is a computable function, T, such that given any Gödel number, e_f, for a computable function, f, and any natural number,p, we have T(n_f, p) = f(p). This idea is captured, and generalized, in a URS as follows:

We are given

U, a set
o: UxU --> U, a total function (which we will call the "dot function")
alpha U
phi U
* U

Let V = U-{*}, then the above data is required to satisfy the following axioms:

o(*,u) = * = o(u, *) for all u U
o(o(alpha, x), y) V and o(o(o(alpha, x), y), z) = o(o(x,z), o(y,z)) for all x,y,z V
o(o(o(phi, a), b), c) V and
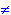o(o(o(o(phi, a), b), c), d) = c if a=d

for all a,b,c,d

The intuition here is that every element of u

U can also be viewed as a partial mapping from U to U , namely the mapping taking each w

U to o(u, w) where the special element, *, is interpreted as "undefined" . Indeed we can do more, for every n

N we can also interpret each u

U as a partial mapping from Uⁿ to U , namely the mapping taking (w_1,...,w_n)

Uⁿ to o(...o(o(u, w₁), w₂),...), w_n).

The URSA-minor Language

The URSA-minor language is a URS with the number and string data types built-in. The underlying set consists of the integers, the strings and special objects, including the alpha and phi, corresponding to certain built-in functions. More precisely, this is a URS where
the set V is given as follows

The set, N, of Java-Script numbers is a subset of V
The set, S, of Java-Script strings is a subset of V
If n1 N, s1 S, and v1,v2,v3V, then so are:

That is all the elements of V

The ``dot-function'', dot, is defined as follows:

Let n1, n2 N, s1,s2S, and v1, v2, v3, v4V, then

dot([URSerror, v1) = [URSerror]
dot(n1, v1) = n1
dot(s1, v1) = s1
dot([alpha], v1) = [alpha, v1]
dot([alpha, v1], v2) = [alpha, v1, v2]
dot([alpha, v1, v2], v3) = dot(dot(v1, v3), dot(v2, v3))
dot([phi], v1) = [phi, v1]
dot( [phi, v1], v2) = [phi, v1, v2]
dot( [phi, v1, v2], v3) = [ph, v1, v2, v3]
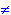dot( [phi, v1, v2, v3], v4) = v3 if v4=v1

dot( [add], n1) = [add, n1]
dot( [add, n1], n2) = n1+n2 (the numerical sum)
dot( [mult], n1) = [mult, n1]
dot( [mult, n1], n2) = n1*n2 (the numerical product)
dot( [suc], n1) = n1+1
dot( [prd], n1) = n1-1
dot( [leq0], n1) = 0 if n10

dot( [concat], s1) = [concat, s1]
dot( [concat, s1], s2) = s1.s2 (the concatenation of the strings)
dot( [idx], s1) = [idx, s1]
dot( [idx, s1], s2) = the index of s2 in s1 (-1 if s2 is not a substring of s1)
dot( [chat], s1) = [chat, s1]
dot( [chat, s1], n1) = the character at position n1 in s1.
dot([len], s1) = the length of the string s1
dot([subst], s1) = [subst, s1]
dot( [subst, s1], n1) = [subst, s1, n1]
dot( [subst, s1, n1], n2) = the substring of s1 beginning at index n1 and ending at index n2.
all other expressions dot(v1, v2) = [URSerror]

Exercises:

Try the following examples of the built-in operations on the calculator (copy the expression and paste it onto the INPUT of the calculator and then click on the PERFORM button on the calculator)

dot( [suc], 17)
dot( [prd], 17)
dot(dot( [add], 21), 33)
dot(dot([add], 3.7), 1.25)
dot(dot([mult], 21), 33)
dot(dot([mult], 3.7), 1.25)
dot(dot([concat], "fish"),"fry")
dot(dot( [idx], "fish"),"is")
dot(dot( [chat], "fish"), 1)
dot(dot(dot([subst], "The beginning of it all"),4),9)
dot([len], "The beginning of it all")

Try editing some of the examples by changing the numerical and string arguments and then performing them again.
Try some of these expressions involving alpha and phi.

dot(dot(dot(dot( [phi], 11), 12), 13), 14)
dot(dot(dot(dot( [phi], 14), 12), 13), 14)
dot(dot(dot(dot(dot(dot([phi], 13),[mult]), [add]), 14), 5), 7)
dot(dot(dot(dot(dot(dot( [phi], 14),[mult]), [add]), 14), 5), 7)
dot(dot(dot([alpha], [add]), [suc]), 12)

Try editing some of the examples by changing the numerical arguments and then performing them again.

What makes it possible to use the language URSA-minor, is that we can use it to define "mappings" which we can name (i.e., assign to a variable) and then use to define still other "mappings". Here is a sequence of such definitions -- all these examples have been "built-into" the system so you do not have to copy them.

Given any vV we can define a "mapping" k_v such that for every xV, dot( k_v, x) = v.
Take k_v = dot(dot(dot( [phi], v), v), v).

Note: From a mathematical point of view it is important to realize that neither the identifier k_v nor the expression dot(dot(dot( [phi], v), v), v) are in V. However, the expression evaluates to an element of V which has been assigned to the identifier k_v. Furthermore, should you wish to define a mapping of your own invention and give it a name you can do so in just this fashion (be advised, however, that your definitions will not survive from session to session, indeed they will not even survive a reloading of the frame).

There exists an identity " mapping", that is a "mapping" id such that for every xV we have dot(id, x) = x
Take id = dot([alpha], dot(dot([phi], 0),0), k_0)

There is a uniform way to compute k_v, that is, we can define a "mapping" beta such that for every vV, dot(beta,v) = k_v.
Take beta = dot(dot([alpha], dot(dot([alpha], [phi]), id)), id)

There is a uniform way to compose "mappings", that is, there exists a mapping gamma such that for all f,g,xV, dot(dot(dot(gamma, f), g), x) = dot(f, dot(f, x)).
Take gamma = dot(dot([alpha], dot(beta, [alpha])), beta)

gamma_2 = dot(dot(gamma, gamma), gamma)

alpha_2 = dot(dot(gamma, alpha), dot(gamma, alpha))

beta2 = dot(dot(gamma, beta),id)

u_2_1 = beta

u_2_2 = dot(beta, id)

References

Eric G. Wagner, Uniformly Reflexive Structures: Towards an Abstract Theory of Computability, Doctoral Dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy, in the Faculty of Pure Science, Columbia University, (1963)
Eric G. Wagner, Gödelizations and Relative Computability, Trans. AMS, 144, (1969) pp 1--41.

top