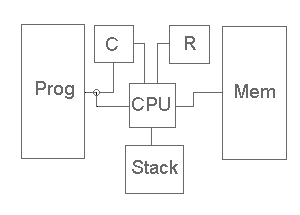
In this chaper we will introduce a simple model of a computer,
the STACKM. In the next chapter we will show how a program
that compiles abstract LANG1
programs into programs for STACKM
can again be presented as a homomophism between appropriate algebras.

The contents of the memory, Mem, can be viewed as a partial function
from the set Id = {a, b, c, ...., z}
of identifiers to the set Val =
Z ![]() {true, false} of integers and booleans. Equivalently, we can
view it as a (subarray of a) JavaScript array of the form
[["a", va], ["v". vb],..., ["z", vz]],
where for each i
{true, false} of integers and booleans. Equivalently, we can
view it as a (subarray of a) JavaScript array of the form
[["a", va], ["v". vb],..., ["z", vz]],
where for each i![]() Id,
vi.
Id,
vi. ![]() Val=
Z
Val=
Z ![]() {true, false}.
{true, false}.
The contents of the stack, Stack, can be viewed as a string on the set Val, i.e. an element of Val*.
The contents of the register, R, is an element of the set Val.
The contents of the counter, C, is a positive integer indicating the number of the current instruction (its location in the string of instructions that constitute the program)
We may think the machine as operating be repeating the following steps
z, for zHere is a typical StackM program together with a corresponding flow diagram (written using assignment statements, etc.) Note that we have numbered the instructions to make it easier to interpret the program.Z, (puts the integer z on the stack and increases the contents of C by 1)
b, for b
{true, false}, (puts the boolean b on the Stack and increases the contents of C by 1)
get(i), for i
Id = {a,b,c,...,z} (puts the current value of the identifer i in Mem onto the stack and increases the contents of C by 1)
put(i), for i
Id = {a,b,c,...,z} (Removes the top element on Stack and puts that value into memory location i in Mem and increases the contents of C by 1)
frR (puts the contents of the register R onto Stack and increases the contents of C by 1)
toR (Removes the top element from Stack, puts that value into the register R and increases the contents of C by 1)
add (Removes the two top elements from Stack, adds them together, puts the result on Stack and increases the contents of C by 1)
mult (Removes the two top elements from Stack, multiplies them together, puts the result on Stack and increases the contents of C by 1)
nand (Removes the two top elements from Stack, nands them together, puts the result on the Stack and increases the contents of C by 1) -- note, nand(b,b') = not(b and b')
neg (removes the top element from Stack, negates it (integer negation), puts the result on Stack and increases the contents of C by 1)
leq (Removes the two top elements from the Stack, if the second element is greater than the first then "true" is put on the stack, otherwise false is put on Stack, then the contents of C is increased by 1)
branch(n), for n
N+ = {1,2,3,....} (removes the top element on the Stack, then, if it is "true" the value of the contents of C changes to n, otherwise the contents of C are increased by 1)
If the above definitions do not make sense (e.g., if the stack has too few elements, the stack of elements of the wrong type, or if C is changed to a value greater than the length of the program) then the machine stops. There are two stopping modes:
- Program Errors: For example, arrival at a state where the stack has too few elements or elements of the wrong type. These will probably result in a Java Script error which we can regard as a "crash" by STACKM. We will be able to show that the compiler does not produce programs that cause STACKM to "crash".
- Program Termination: This will occur only if a state is reached in which the contents of C are greater than the length of the program. This will be the way in which compiled programs will halt. It will also be the basis of the LANG1Syn-algebra structure that we impose on the set of STACKM programs.
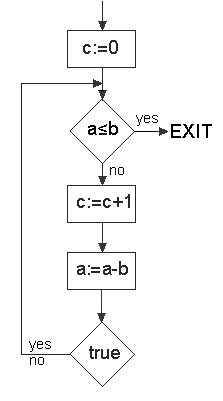
Assuming we start this program in a state in which C = 1 and in a memory state in which "a" has value n and "b" has value p with n,p
1 0
2 put(c)
3 get(a)
4 get(b)
5 leq
6 branch(18)
7 get(c)
8 1
9 add
10 put(c)
11 get(a)
12 get(b)
13 neg
14 add
15 put(a)
16 true
17 branch(3)
get(a)Memory states are also written as JavaScript arrays of identifier/value pairs with 0 as the default value. E.g., as in our treatment of LANG1 states, we write [["a", 7], ["b", 2]] to denote the state s:Id
get(b)
mult
put(c)
Example 1:
Here is a simple straight-line program that multiplies the values given
for the identifiers "a" and "b" and assigns the result to "c". To
"load the program" just click on the perform button. The program
can be run in several different ways -- see directions below the calculator.
Example 2: The program in this example is the one shown above for division. It divides the value of identifier "a" by the value of identifier "b" and assigns the integer part of the result to identifier "c" and the remainder to identifier "a". Executing the program with the given arguments (memory) takes 51 steps. Remember, you must load the program (by clicking on the perform button) before trying to run it. Then clear the input and enter runSTM(51). Or, you can enter, say, runSTM(10) and click "perform" six times.
Now try writing and running your own programs!