Trees over Signatures
Earlier we defined the set of <S,  >-terms
for a signature <S,
>-terms
for a signature <S,  >.
It
is sometimes convenient to replace the set of <S,
>.
It
is sometimes convenient to replace the set of <S,  >-terms
by the set of <S,
>-terms
by the set of <S,  >-trees.
. Informally speaking, a <S,
>-trees.
. Informally speaking, a <S,  >-tree
is a special kind of picture labeled with elements of
>-tree
is a special kind of picture labeled with elements of  in a manner that is compatible with the structure of
in a manner that is compatible with the structure of  (the arities and sorts match up correctly). For example, here is
an informal SigP-tree
(the arities and sorts match up correctly). For example, here is
an informal SigP-tree
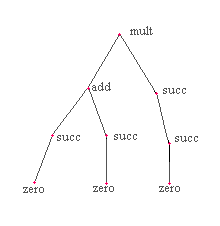 The picture is compatible with the structure of
The picture is compatible with the structure of  in that the nodes labelled with operators that have n arguments have exactly
n "downward" edges issuing from that node. While such pictures are
clearly easy to see, it is not all that obvious how to view them as mathematical
objects. Indeed there are many ways to give a formal definition of
such a tree and we will see several of them before this book is done.
However, for our present purposes we will use the the following formal
definition. This definition is easy to work with mathematically,
it is easy to generalize in various ways (e.g., to define infinite trees),
and will provide our first example of an algebra in which the carriers
consist of functions.
in that the nodes labelled with operators that have n arguments have exactly
n "downward" edges issuing from that node. While such pictures are
clearly easy to see, it is not all that obvious how to view them as mathematical
objects. Indeed there are many ways to give a formal definition of
such a tree and we will see several of them before this book is done.
However, for our present purposes we will use the the following formal
definition. This definition is easy to work with mathematically,
it is easy to generalize in various ways (e.g., to define infinite trees),
and will provide our first example of an algebra in which the carriers
consist of functions.
Definition:
Given a signatuare <S,  >,
we define a tree over <S,
>,
we define a tree over <S,  >to
be a partial mapping t:[N]*
>to
be a partial mapping t:[N]*
 with the following properties
with the following properties
-
For all w
 [N]*
and j
[N]*
and j [N],
if t( w
[N],
if t( w i)
=
i)
= 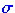

 v,s
then there exists n,
j
v,s
then there exists n,
j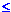 n, and u
n, and u Sn,
q
Sn,
q S and
S and 

 u,q
such that uj = s and t(v)=
u,q
such that uj = s and t(v)=  .
.
-
For all v
 [N]*,
if t(v) =
[N]*,
if t(v) = 

 u,swhere
|u|= n then, for each i
u,swhere
|u|= n then, for each i {1,...,n},
t(v
{1,...,n},
t(v i) is defined
i) is defined
-
t is defined on a finite, non-empty subset
of [N]*
Example: The tree, t:[N]* SigP,
such that t takes
SigP,
such that t takes
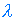 to mult
to mult
1 to add
2 to succ
11 to succ
12 to succ
21 to succ
111 to zero
121 to zero
211 to zero
and is otherwise undefined
This, tree t can be drawn as follows:
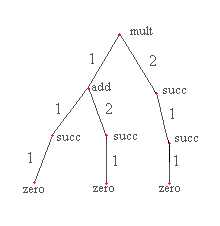
This is the same tree as we had before except we have added labels on the
edges. Note that if you follow down a path from the root of
the tree (the topmost node in the picture) that the string (sequence)
of edge-labels that you encounter on the way to a node is exactly the index
of that node, i.e., the string s such that t(s) is the label of that node.
end
For any signature <S,  >
there is a one-to-one correspondance between <S,
>
there is a one-to-one correspondance between <S,  >-trees
and <S,
>-trees
and <S,  >-terms.
For example, the SigP-term
>-terms.
For example, the SigP-term
mult(add(succ(zero( )), succ(zero( ))), succ(succ(zero(
))))
corresponds to the above SigP-tree,
t. This correspondence between <S,  >-trees
and <S,
>-trees
and <S,  >-terms
is actually the underlying mapping of the initial homomorphism from T
>-terms
is actually the underlying mapping of the initial homomorphism from T and the appropriate algebra of <S,
and the appropriate algebra of <S,  >-trees.
>-trees.
The algebra treealg
The signature of treealg is: sigP
The carriers of treealg are:
[""]// The set of SigP-trees.
The operations of the algebra treealg are:
["zero", "treezero()"]
["succ", "treesucc(arg[1])"]
["pred", "treepred(arg[1])"]
["add", "treeadd(arg[1], arg[2])"]
["mult", "treemult(arg[1], arg[2])"]
End of algebra treealg
where
-
treezero() is the function of no arguments which returns the SigP-tree,
t where for w
 [N]*,
t(w) = "zero" if w=
[N]*,
t(w) = "zero" if w=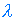 and is otherwise undefined.
and is otherwise undefined.
The corresponding JavaScript function is:
function
treezero() {
return Function("node", "if (node=='') {return 'zero'}")}
The JavaScript program does not return a mathematical function pe se,
but it does return a JavaScript function that implements the desired function.
-
treesucc( t1 ) is the function of one argument, a tree, which returns
a new tree, t, where for w
 [N]*,
[N]*,
t(w) = "succ" if w=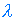
t(w)
= t1(u) if w = 1 u
u
undefined
otherwise
The corresponding JavaScript function is:
function treesucc(nn1)
{
return Function("node",
"if (node=='') {return 'succ'} else {if (node.charAt(0)=='1') {var bb=
" + nn1 + "(node.substring(1, node.length)); return bb}}") }
-
treepred( t1 ) is the function of one argument, a tree, which returns
a new tree, t, where for w
 [N]*,
[N]*,
t(w) = "pred" if w=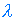
t(w)
= t1(u) if w = 1 u
u
undefined
otherwise
The corresponding JavaScript function is:
function treepred(nn1)
{
return Function("node",
"if (node=='') {return 'pred'} else {if (node.charAt(0)=='1') {var bb=
" + nn1 + "(node.substring(1, node.length)); return bb}}") }
NOTE, in reading this program and the following
programs, you must distinguish between double single quote ('') and single
double quote (")
-
treeadd(t1, t2) is the function of two arguments, both SigP-trees,
which returns a new tree, t, where for w
 [N]*,
[N]*,
t(w)
= "add" if w=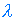
t1(u)
if w = 1 u
u
t2(u)
if w = 2 u
u
undefined
otherwise
The corresponding JavaScript function is:
function
treeadd(nn1, nn2) {
return Function("node", "if (node=='') {return 'add'} else {if (node.charAt(0)=='1')
{var bb= " + nn1 + "(node.substring(1, node.length)); return bb} else {if
(node.charAt(0)=='2') {var bb= " + nn2 + "(node.substring(1, node.length));
return bb}}}");}
-
treemult(t1, t2) is the function of two arguments, both SigP-trees,
which returns a new tree, t, where for w
 [N]*,
[N]*,
t(w)
= "mult" if w=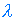
t1(u)
if w = 1 u
u
t2(u)
if w = 2 u
u
undefined
otherwise
The corresponding JavaScript function is:
function
treemult(nn1, nn2) {
return Function("node", "if (node=='') {return 'mult'} else {if (node.charAt(0)=='1')
{var bb= " + nn1 + "(node.substring(1, node.length)); return bb} else {if
(node.charAt(0)=='2') {var bb= " + nn2 + "(node.substring(1, node.length));
return bb}}}");}
The corresponding SigP-algebra for the UA-Calculators
is named "treealg". To see that the corresponding initial homomorphism
translates from SigP-expressions to SigP-trees
you can test it with the following UA-calculator. Since the
actual algebra is over JavaScript functions (i.e., JavaScript programs
returning a value) rather than abstract functions it is best to check the
results by looking at application of these "functions" to specific arguments.
In the following calculator the initial expression applies the function
to the empty string, "". You can change
this argument to see the effect -- for example applying it to the argument
"21" will return "succ" , while applying it to the argument
"321" will return "undefined" in keeping with the fact that the corresponding
abstract function is undefined for that argument.
As you can see by inspection, the tree we have here is exactly the one
used earlier as an example.
![]() >-terms
for a signature <S,
>-terms
for a signature <S, ![]() >.
It
is sometimes convenient to replace the set of <S,
>.
It
is sometimes convenient to replace the set of <S, ![]() >-terms
by the set of <S,
>-terms
by the set of <S, ![]() >-trees.
. Informally speaking, a <S,
>-trees.
. Informally speaking, a <S, ![]() >-tree
is a special kind of picture labeled with elements of
>-tree
is a special kind of picture labeled with elements of ![]() in a manner that is compatible with the structure of
in a manner that is compatible with the structure of ![]() (the arities and sorts match up correctly). For example, here is
an informal SigP-tree
(the arities and sorts match up correctly). For example, here is
an informal SigP-tree

![]() >,
we define a tree over <S,
>,
we define a tree over <S, ![]() >to
be a partial mapping t:[N]*
>to
be a partial mapping t:[N]*![]()
![]() with the following properties
with the following properties
to mult
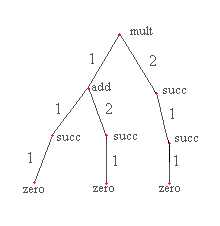
![]() >
there is a one-to-one correspondance between <S,
>
there is a one-to-one correspondance between <S, ![]() >-trees
and <S,
>-trees
and <S, ![]() >-terms.
For example, the SigP-term
>-terms.
For example, the SigP-term