Preliminaries

While we assume that the reader has a good working knowledge of concepts such as sets and functions, we still need to establish some basic notation and present precise mathematical definitions for some familiar concepts that are sometimes only treated informally. The precision will make it easier to make some definitions and prove some results. However, the reader can decide when, and if, to go over this material.

Some typographic conventions
Some basic notation
Ordered Pairs
Total and Partial Functions
Strings
S-ary sets and S-ary mappings
Commuting Diagrams

Some Typographic conventions

Mathematical symbols are written in blue, see examples below.
Text that can be copied to, and performed on, UA-calculators is written in green.

Some basic notation

N denotes the set of natural numbers {0,1,2,...}
[N] denotes the set of positive natural numbers {1,2,3,... }
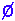[n], for nN, denotes the set {1,...,n}. In particular, [0] = , the empty set.
Z denotes the set of integers { ...-1, 0, 1,... }

Ordered Pairs

We will have many occasions where we will want to talk about ordered pairs of elements from a set, X. Given x,y

X, we will write <x, y> for the ordered pair with first element x andsecond element y. The significant property of ordered pairs is that for any two ordered pairs <x,y> and <u,v> from a set X that we have <x,y> = <u,v> if, and only if x=u and y=v

Note that, we have not said what an ordered pair is, we have only stated what we require of it. This is enough for most purposes -- as long as you are willing to accept the existence of such things. However, for the sake of completeness we can define <x,y> as the set {x, {x,y}}. This is thedefinition used in many approaches to set theory.

Exercise: Show that defining <x,y> as {x,{x,y}} works, i.e., that it satisfies the above property.

Total and Partial Functions

Definition: Given sets A and B a total function, f, from A to B consists of the following data

The set A, called the source of f
The set B, called the target of f
graph(f), a subset of AB with the property that for every aA there exists exactly one bB such that <a,b>graph(f). We call graph(f) the graph of f.

We write f:A

B as an abbreviation for "f is a total function from A to B". We write f(a) to denote the unique element of B such that <a, f(a)>

f
end

Definition: Given sets A and B a partial function, f, from A to B consists of the following data

The set A, called the source of f
The set B, called the target of f
dom(f), a subset of A, called the domain of f
fun(f), a total function from dom(f) to B.

We write f:A

B as an abreviation for "f is a partial function from A to B". We write f(a) to denote the unique element of B such that <a, f(a)> is an element of the graph of fun(f) -- note, this implies that a

dom(f).
end

Definition: Given total functions f:AB and g:BC we define their composite, written as gf : AC, to be the total function from A to C with graph { <a,c> | there exists bB such that <a,b>graph(f) and <b,c> graph(g)}.

Given partial functions f:AB and g: BC we define their composite, written as gf : AC, to be the partial function from A to C with

dom(gf) = { a | adom(fun(f)), and fun(f)(a)dom(fun(g)) }
graph(fun(.gf)) = { <a,c> | adom(gf) and fun(g)(fun(f)(a)) = c }

end

Definition: If f:AB then we define the image of f , denoted Im(f), to be { b B | there exists aA, such that <a,b>graph(f)}
end

Strings

Strings play a basic role in computer science. However the concept is often treated very informally with a string being regarded as a sequence of symbols written on a page. While this informal idea is sufficient for many purposes, we will find it useful, and perhaps essential, to replace it with a more mathematically precise construct.

Definition: For any set A, a string over A of length n is a mapping u:[n]A.
Given a string u over A of length n we sometimes write it as u = u₁u₂u_n where u_i = u( i ).
Let A* denote the set of all strings over A.
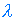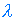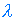Let denote the unique string (mapping) :[0]A, we call the empty string. We may sometimes write "" rather than
Given any uA* let |u| denote the length of u, so, u:[|u|]A.
For any u, vA* let uv denote their concatenation, that is the string

v :[|u|+|v|]

A
i

u(i) if i

|u|
i

v(i-|u|) if i>|u| end

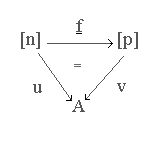
Definition: Given strings u:[n]A and v:[p]A, a string morphism f:uv is a mapping f : [n][p] such that vf = u

S-indexed sets, S-ary Sets, and S-ary Mappings

Given a set S, it is quite common to speak of S-indexed sets, or sets whose elements are indexed by S. The usual notation for an S-indexed set A would be either A = < a_s | s

S> or A = { a_s | s

S }. I prefer the former notation over the latter notation for the simple reason that an indexed set is not just a set, but a set "with indexing". While two sets are equal if, and only if, they have the same elements, there are good reasons for saying that two indexed sets are the same if, and only if, they have the same indexing. For example, if we speak of points in an n-dimensional space as being [n]-indexed sets of real numbers (commonly called real vectors) then the order (given by the indexing) is clearly important since two points are the same if, and only if, they have the same values at the same indices. On the other hand, the notation A = { a_s | s

S }suggests that A is just a set and that the indexing need not be considered. Despite all these complications, the notion of an S-indexed set is commonly used without bothering to define it. What then is the definition of an S-indexed set?

Definition: Given sets S and U an S-indexed set A of elements of U is the graph of a mapping SU .
end

We shall make considerable use of a specialization of the notion of an S-indexed set, that we call an S-ary set.

Definition: Given a set S, and S-ary set is an S-indexed set of sets (n.b., it is not clear what to take for U as there is no set of all sets).
Given S-ary sets A = < A_s | sS> and B = < B_s | sS> we define an S-ary mapping f:AB to be an S-indexed set of mappings f = < f_s:A_sB_s | sS>.
end

Commuting Diagrams

A diagram is a directed graph in which the nodes are labeled with names of sets and whose edges are labeled with names of functions. A diagram is said to be a commuting diagram if for every ordered pair of nodes in the diagram, if we compose the functions along each path from the first node to the second then we always get the same result. Such a diagram is a convenient way to present various equalities. For example, we used the diagram

in the definition of string morphism to illustrate that v

f = u Sometimes, as in this example, an equals sign, "=", is inserted in the diagram to indicate that it is a commuting diagram, but this is not mandatory. Here is another example:

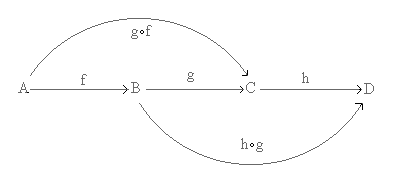This commuting diagram asserts the commutativity of functional composition, i.e., that h

f) = (h