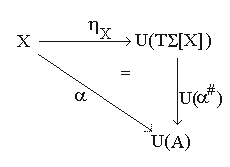Free Algebras, Derived Operations and Substitution
In the section on initial algebras we introduced the concept of an <S, >-term
(reference). Those terms,
sometimes called ground terms, contain only symbols from
>-term
(reference). Those terms,
sometimes called ground terms, contain only symbols from  .
We now want to extend that concept to the idea of <S,
.
We now want to extend that concept to the idea of <S, >-terms
with variables. To do this we introduce the important concept
of a free <S,
>-terms
with variables. To do this we introduce the important concept
of a free <S, >-algebra
generated by an S-indexed set of sets,X
>-algebra
generated by an S-indexed set of sets,X
The essential theoretical core is the following
Given an S-sorted signature <S, >
and an S-indexed set X
= <Xs | s
>
and an S-indexed set X
= <Xs | s S>
with Xs
S>
with Xs
 "",s=
"",s= 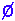 for all s
for all s S,
we can form a new S-sorted signature <S,
S,
we can form a new S-sorted signature <S,  (X)>
with
(X)>
with
 (X)"",s
=
(X)"",s
=  s
s Xs
Xs
 (X)w,s
=
(X)w,s
=  w,s,
for all w
w,s,
for all w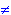 "".
"".
Let T (X)
be the initial <S,
(X)
be the initial <S,  (X)>-algebra.
We can view T
(X)>-algebra.
We can view T (X)
as an <S,
(X)
as an <S,  >-algebra,
T
>-algebra,
T [X],
by simply not viewing the elements from X
as new constant operators but keeping everything else the same, that
is we take:
[X],
by simply not viewing the elements from X
as new constant operators but keeping everything else the same, that
is we take:
T [X]s
= T
[X]s
= T (X)s
(X)s
and
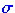 T
T [X]
=
[X]
= 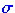 T
T (X).
(X).
for all 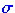

 .
.
Definition: The
<S, >-algebra
T
>-algebra
T [X]
is called "the" <S,
[X]
is called "the" <S,  >-algebra
freely generated by X. The
<S,
>-algebra
freely generated by X. The
<S,  (X)>-terms
that make up the carriers of T
(X)>-terms
that make up the carriers of T [X]
,
are called derived operators.
[X]
,
are called derived operators.
end
The <S,  >-algebra
freely generated by X has the following
important property.
>-algebra
freely generated by X has the following
important property.
Theorem: Let A
be any
<S,  >-algebra,
then for any S-indexed family of mappings,
>-algebra,
then for any S-indexed family of mappings, = <
= <  s:Xs
s:Xs As | s
As | s S>
there is a unique homomorphism
S>
there is a unique homomorphism  #:T
#:T [X]
[X] A that extends
A that extends  in the sense that if we let
in the sense that if we let 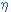 X
be the S-indexed family of inclusion mappings
X
be the S-indexed family of inclusion mappings 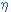 X
= <
X
= < 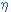 X,s:Xs
X,s:Xs T
T [X]s
|
s
[X]s
|
s S> then
S> then  #s
#s
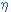 X,s
=
X,s
=  s for
all s
s for
all s S
(i.e., for each x
S
(i.e., for each x Xs
Xs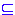 T
T [X]s
,
[X]s
,  #s(x)
= =
#s(x)
= =  s(x)).
s(x)).
Proof: Given  ,
extend A as a <S,
,
extend A as a <S,  (X)>-algebra,
A+,
where for each s
(X)>-algebra,
A+,
where for each s S
and x
S
and x Xs,
xA =
Xs,
xA =  s(x).
Then, since T
s(x).
Then, since T (X)
is
the initial
(X)
is
the initial  (X)-algebra
there exists a unique homomorphism h:T
(X)-algebra
there exists a unique homomorphism h:T (X)
(X) A+.
But since T
A+.
But since T [X]
is
just T
[X]
is
just T (X)
with the elements of X no longer treated as
operators, it follows that U(h) also
gives us a <S,
(X)
with the elements of X no longer treated as
operators, it follows that U(h) also
gives us a <S,  >-homomorphism
>-homomorphism  #
:T
#
:T [X]
[X]  A with the property that
A with the property that  #s
#s
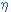 X,s
=
X,s
=  s for
all s
s for
all s S.
The homomorphism is unique for if
S.
The homomorphism is unique for if  :T
:T [X]
[X]  A with
A with  s
s
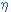 X,s
=
X,s
=  s
for all s
s
for all s S,
then U(
S,
then U( )
would give us a homomorphism h":T
)
would give us a homomorphism h":T (X)
(X) A+
which implies h" = h, by the initiality
of h, but then U(
A+
which implies h" = h, by the initiality
of h, but then U( )
= U(h) = U(
)
= U(h) = U( ) so
) so =
=  .
.
end
The statement of the above theorem can be done a little more neatly
if , for any <S,  >-algebra
A, we define U(A) to be the corresponding
S-indexed
set of its carriers and for any homomorphism h:A
>-algebra
A, we define U(A) to be the corresponding
S-indexed
set of its carriers and for any homomorphism h:A B
we define U(h) to be the S-indexed
mapping U(h)=< hs:As
B
we define U(h) to be the S-indexed
mapping U(h)=< hs:As Bs
| s
Bs
| s S> used to define the
homomorphism h. Given this additional
notation we can state the theorem as follows:
S> used to define the
homomorphism h. Given this additional
notation we can state the theorem as follows:
Let X be an S-indexed
set of variables and let 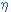 X
be the S-indexed family of inclusion mappings
X
be the S-indexed family of inclusion mappings 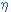 X
= <
X
= < 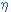 X,s:Xs
X,s:Xs T
T [X]s
then
for any
<S,
[X]s
then
for any
<S,  >-algebra,
A,
and S-indexed map
>-algebra,
A,
and S-indexed map :X
:X U(A)
there is a unique homomorphism
U(A)
there is a unique homomorphism  #:T
#:T [X]
[X] A such that
A such that  #
#
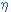 X
= h. This equality can be expressed by the following
commuting diagram
X
= h. This equality can be expressed by the following
commuting diagram
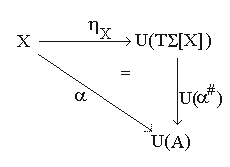
We now turn to the applications of the above result:
Given a signature <S, >,
an S-sorted set of variables X
and an <S,
>,
an S-sorted set of variables X
and an <S, >
-algebra A the above result provides a precise
meaning of what it means to interpret a derived operator as a function
.
>
-algebra A the above result provides a precise
meaning of what it means to interpret a derived operator as a function
.
Definition: Given a derived
operator t (i.e., an <S,  (X)>-term
t) then for any <S,
(X)>-term
t) then for any <S, >
-algebra A, we define the derived operation,
tA, to be the function such that, for any assignment,
h,
of values in A to the elements of X
(i.e., any any
S-indexed family of mappings,
h = < hs:Xs
>
-algebra A, we define the derived operation,
tA, to be the function such that, for any assignment,
h,
of values in A to the elements of X
(i.e., any any
S-indexed family of mappings,
h = < hs:Xs As | s
As | s S> )
we define tA(h) = h#(t).
S> )
we define tA(h) = h#(t).
end
Example:
Recall the Signature sigP in programming
form:
name: sigP
sorts: {int}
operators:
zero: -->int
pred:int-->int
succ:int-->int
add:int.int-->int
mult:int.int-->int
End of signature sigP.
There is only one sort in this signature. So let X
be the 1-sorted set X = {x1, x2, x3}.
Then a typical <1, SigP(X)>-term,
t, would be the following:
t = "add(pred(x2(
)), succ( succ(x1( ))))".
Note, that we are treating the variables
(the elements of X) as <1,
SigP(X)>-terms and are thus writing "x1(
)" rather than just "x1".
Now say we want to interpret this term in the algebra alg_A
where
-
Aint = Z
-
zeroA = 0
-
predA(z) = z-1
-
succA(z) = z+1
-
addA(z, z') = z+z'
-
multA(z, z') = z*z'
Then we claim that evaluating (interpreting) the above term,
t, with x1 = 2,
x2= 5, and x3=7 is exactly the
same as taking h#(t) for
h:X Aint
such that h(x1)=2, h(x2)=5
and h(x3)=7.
Aint
such that h(x1)=2, h(x2)=5
and h(x3)=7.
end
Performing Derived Operators on the UA-Calculators
Just as we were able to use the function aitch to compute the unique
homomorphism from an initial
<S, >-algebras
to an arbitrary <S,
>-algebras
to an arbitrary <S, >-algebra
on the UA-calculator, so can we can use the function aitchFree
to compute the unique homomorphism h#
for a combination of the <S,
>-algebra
on the UA-calculator, so can we can use the function aitchFree
to compute the unique homomorphism h#
for a combination of the <S, >-algebra
generated by X and an assignment
h:X
>-algebra
generated by X and an assignment
h:X A on
the UA-calculator. The function aitchFree takes three arguments:
A on
the UA-calculator. The function aitchFree takes three arguments:
-
the name of the algebra
-
an arrays of pairs of strings specifying the assignment
of values to the variables
-
the term-with-variables to be evaluated
Try the following example:
To convince yourself that everything is on the up-and-up,
try some variations:
-
make modifications on the term and perform it again
-
try other algebras with the same signature ( the algebras "alg_B",
"alg_C", "alg_D" and "alg_E" with signature SigP are built into the calculator,
click
here to review their descriptions). Note that
the above expression will not evaluate in algebras alg_D and alg_E since
these algebras don't have numerical carriers.
-
The algebra alg_D has the booleans as its carrier -- try evaluating the
expression:
aitchFree("alg_D", [["x1",
"'true'"], ["x2", "'false'"], ["x3", "'true'"]], "add(pred(x2( )),
succ(succ(x1( ))))")
-
The algebra alg_E has strings on the set {a,b,...,x,A,B,...,Z}
as its carrier -- try evaluating the expression
aitchFree("alg_E",
[["x1", "'abc'"], ["x2", "'ed'"], ["x3", "'uvw'"]], "add(pred(x2(
)), succ(succ(x1( ))))")
Note These expressions can be copied to the
above calculator in the usual manner -- however, recall that if your
browser displays them on more than one line then the copy may not run until
you delete the hidden characters at the ends of the lines.
Note that in both
examples the values in the assignment are written using both a double and
a single quote -- the double quotes are used for all assignments, the single
quotes indicate that the value is a string.
Derived Operators and Substitution
Substitution of terms within terms is a very common operation within many
areas in computer science. Despite this, it is often treated extremely
informally and this makes it difficult to prove even seemingly obvious
results such as that substitution is associative. However,
by using the idea of free algebras we can give a rigorous definition of
substitution and prove the associativity of substitution by applying the
above theorem.
Definition: Given an <S,  (X)>-term
t and an assignment,
(X)>-term
t and an assignment,  ,
of <S,
,
of <S,  (Y)>-terms
to the elements of X, that is, an
S-indexed mapping
(Y)>-terms
to the elements of X, that is, an
S-indexed mapping  :X
:X  U(T
U(T [Y]),
we define the result of substituting
[Y]),
we define the result of substituting (x)
for x in
t , for all x
(x)
for x in
t , for all x X,
to be the <S,
X,
to be the <S,  (Y)>-term
(Y)>-term  #(t).
[this is a direct application of the above theorem but with
#(t).
[this is a direct application of the above theorem but with  in place of h].
in place of h].
end
Clearly we can follow one substitution with another, which is
to say, we can compose compositions. The above framework leads us
to the following formal definition of composition.
Definition: Given an <S,  (X)>-term
t , an assignment,
(X)>-term
t , an assignment,  ,
of <S,
,
of <S,  (Y)>-terms
to the elements of X, and an assignment,
(Y)>-terms
to the elements of X, and an assignment,  ,
of <S,
,
of <S,  (Z)>-terms
to the elements of Y, then we define their
composite,
denoted
(Z)>-terms
to the elements of Y, then we define their
composite,
denoted 

 ,
to be the assignment U(
,
to be the assignment U( #)
#)
 :X
:X  U(T
U(T [Z]),
where "
[Z]),
where " " denotes the composition
for S-indexed mappings.
" denotes the composition
for S-indexed mappings.
end
Note: We could use just one
symbol for both composition of assignments and composition of S-indexed
mappings and write

 =U(
=U( #)
#)
 ,
since the two uses can be distinguished by context. Such overloading
is commonly used in mathematical treatments for the sake of brevity, but
it comes at a price.
,
since the two uses can be distinguished by context. Such overloading
is commonly used in mathematical treatments for the sake of brevity, but
it comes at a price.
Proposition: The above composition
is associative. that is, given an assignment  ,
of <S,
,
of <S,  (Y)>-terms
to the elements of X, an assignment,
(Y)>-terms
to the elements of X, an assignment,  ,
of <S,
,
of <S,  (Z)>-terms
to the elements of Y, and an assignment,
(Z)>-terms
to the elements of Y, and an assignment,  ,
of <S,
,
of <S,  (W)>-terms
to the elements of Z, then
(
(W)>-terms
to the elements of Z, then
(

 )
)
 =
= 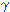
 (
(

 ).
).
Proof: Consider the following
diagram:
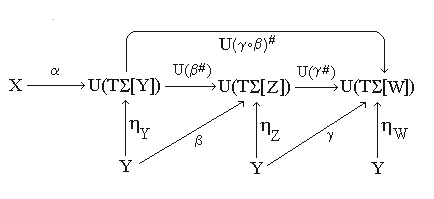 From the theorem on free algebras and the definition of the composite of
assignmnents it follows that
From the theorem on free algebras and the definition of the composite of
assignmnents it follows that
U(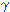 #)
#) U(
U( #)
#)
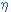 Y
= U(
Y
= U(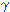 #)
#)
 = (
= (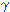

 )#
)#
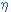 Y
which then implies that
Y
which then implies that 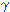 #
#
 #
= (
#
= (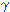

 )#
)#
but then 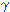
 (
(

 )
=
)
= 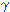
 (
U(
(
U( #)
#)
 )
= U(
)
= U( 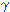 #)
#) (
U(
(
U( #)
#)
 )
= (U(
)
= (U( 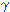 #)
#) U(
U( #))
#))
 = (
= (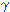

 )#
)#
 = (
= (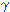

 )
)

end
(X)"",s =
s
Xs
(X)w,s =
w,s, for all w
"".
![]() (X)
be the initial <S,
(X)
be the initial <S, ![]() (X)>-algebra.
We can view T
(X)>-algebra.
We can view T![]() (X)
as an <S,
(X)
as an <S, ![]() >-algebra,
T
>-algebra,
T![]() [X],
by simply not viewing the elements from X
as new constant operators but keeping everything else the same, that
is we take:
[X],
by simply not viewing the elements from X
as new constant operators but keeping everything else the same, that
is we take:
![]() [X]s
= T
[X]s
= T![]() (X)s
(X)s
T
[X] =
T
(X).