Compiling LANG1 into the StackM Language

In this section we will show how to compile LANG1 onto the stack machine StackM by means of a homomorphic compiler. That is, the compiler is given by a homomorphism from the free LANG1Syn-algebra, T_LANG1Syn , to an appropriate LANG1Syn-algebra, CMP, whose carriers of sort <id> is the set, Id, of identifiers and whose carriers of sorts <be>, <ae> and <st> are sets of StackM programs.

Rather than define CMP directly we define a larger, and easier to define, LANG1Syn-algebra, StP, and define CMP to be the subalgebra of StP that is the image of the unique homomorphism, h_StP : T_LANG1SynStP given by the initiality of T_LANG1Syn . Again, by virtue of the initiality of T_LANG1Syn, we have a unique homomorphism h_CMP : T_LANG1Syn CMP. If i:CMPStP is the inclusion homomorphism given by CMP being a subalgebra of StP, it follows from initiality that ih_CMP = h_StP . To show that this is the correct compiler all we have to show is that there is a homomorphism RUN from CMP to LANG1_Sem, for then, by initiality, we have RUN h_CMP = h_SEM , where h_SEM :T_LANG1SynSem (= LANG1Sem) is the homomorphism giving the abstract semantics of LANG1.

In this chapter let ProgS denote the set of all possible StackM programs (set of all strings on the set of instructions)
Recall that the abstract syntax of LANG1 was given by the initial algebra for the signature LANG1Syn with

sorts: {<id>, <be>, <ae>, <st>}

           operations:
           LANG1syn(<id>) = {LANG1var}
           LANG1syn(<be>) = {tr, fa}
           LANG1syn(<ae>) = {LANG1Int}
           LANG1syn(<be>, <be>) = {not}
           LANG1syn(<be>.<be>,<be>) = {and}
           LANG1syn(<ae>.<ae>,<be>) = {eq, leq}
           LANG1syn(<ae>,<ae>) = {succ, pred}
           LANG1syn(<id>,<ae>) = {id2ae}
           LANG1syn(<ae>.<ae>,<ae>) = {add, mult}
           LANG1syn(<id>.<ae>,<st>) = {assign}
           LANG1syn(<st>.<st>,<st>) = {compos}
           LANG1syn(<be>.<st>.<st>,<st>) = {if}
           LANG1syn(<be>.<st>,<st>) = {wdo}

End of signature LANG1syn.

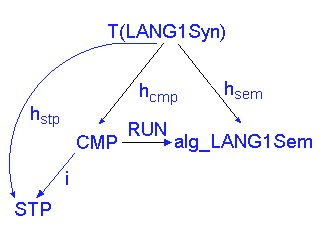
Recall also that the abstract syntax of LANG1 corresponds to the initial LANG1Syn-algebra, T(LANG1Syn), and that the semantics of LANG1 is given by the unique homomorphism, h_SEM :T(LANG1Syn) --> alg_LANG1Sem.

What we want to do in this section is produce a new LANG1Syn-algebra, call it CMP, which is such that

The unique homomorphism, h_CMP :T(LANG1Syn)-->CMP, from the initial LANG1Syn-algebra to CMP, takes each identifier to itself and takes each boolean expression, arithmetic expression and statement to a StackM program which is a compilation of it.

There is a homomorphism RUN :CMP alg_LANG1Sem with the property that RUNh_CMP = h_SEM.

If we are to satisfy the first condition then it is necessary that the carrier CMP_<id> contain the set Id, of identifiers, and that the carriers CMP_<be>, CMP_<ae> and CMP_<st> contain the appropriate subsets of ProgS. Rather than spend a lot of time trying to figure out what we mean by "appropriate subsets" we can take the easy way out and start by defining a super algebra, STP, of CMP.
        STP_<id>= Id
       STP_<be>= ProgS
        STP_<ae>= ProgS
        STP_<st>= ProgS

The operations of STP are then defined as follows:

STP(true)( ) = true
STP(false)( ) = false
STP(not)(be) =
be
toR
frR
frR
nand
STP(and)(be1, be2) =
be1
be2
nand
toR
frR
frR
nand
STP(eq)(ae1, ae2) =
ae1
ae2
leq
ae2
ae1
leq
nand
toR
frR
frR
nand
STP(leq)(ae1, ae2) =
ae1
ae2
leq
STP(id2ae)( id ) = get( id )
STP(neg)( ae ) =
ae
neg

STP(succ)( ae ) =
ae
1
add
STP(pred)( ae )=
ae
1
neg
add
STP(add)(ae1, ae2) =
ae1
ae2
add
STP(mult)(ae1, ae2) =
ae1
ae2
mult
STP(assign) (id, ae ) =
ae
put( id )

To describe the operations corresponding to the statements, compos, if, and wdo, we need two auxilliary functions: len and mod. The function len:ProgS

N takes a StackM program and returns its length (= number of instructions). The function mod:ProgS

NProgS, takes a StackM program, p, and a natural number, n, as arguments and returns a new StackM program, mod( p, n) such that for every i, 1

len(p),

mod(p, n) = branch(q + n) if p( i ) = branch( q ) for some qN
mod(p, n) = p( i ) otherwise (i.e., if p( i ) is not a branch instruction)

STP(compos)(st1, st2) =

st1
mod(st2, len(st1))
STP(if)(be, st1, st2) =
be
branch( len( be )+len( st2 )+4 )
(mod( st2, len( be )+ 1)),
true
branch( len( be )+len( st1 )+len( st2 )+4)
mod( st1, len( be ) +len( st2 ) + 3)
STP(wdo)( be, st ) =
be
branch( len( be )+3)
true
branch( len( be )+len( st )+5)
mod( st, len( be )+ 3)
true
branch( 0 )

Fact: STP is a LANG1Syn-algebra and thus there exists a unique homomorphism h_STP:T_LANG1SynSTP.
end

Definition: Let CMP denote the LANG1Syn-algebra that is the image of h_STP:T_LANG1SynSTP. Let h_CMP:T_LANG1SynCMP be the unique homomorphism from T_LANG1Syn to CMP, and let i:CMP STP denote the inclusion homomorphism from CMP to STP.
end

A Homomorphism, RUN, from CMP to SEM = LANG1Sem

What we will do next is to define the functions that serve as the components of the desired homomorphism RUN. We shall do this by defining an S-ary mapping (for S = {<id>, <be>, <ae>, <st>}) from U(CMP) to U(LANG1Sem). This {<id>, <be>, <ae>, <st>}-ary mapping will not be homomorphism from STP to LANG1Sem but, as we shall see, its restriction to CMP will yield a homomorphism.

Notation: For the sake of brevity let SEM denote alg_LANG1Sem and recall that
         SEM_<id>= Id
       SEM_<be>= the set of all partial mappings SttStt {true, false}
        SEM_<ae>= the set of all partial mappings SttStt Z
       SEM_<st>= the set of all partial mappings SttStt

Now, by definition, Stt is the set of all partial mappings from Id to Z while M is the set of all partial mappings from Id to Val = Z {true, false}

In this section let

M denote the set of all memory states (all total functions m:IdVal)
S    denote the set of all stack states ( all strings on the set Val)
R    denote the set of all possible contents of the register R (all elements of the set Val)
C    denote the set of all possible contents of the instruction counter C (all natural numbers)

end

Definition: Given a StackM program pProgS define run[p] to be the partial function
run[p]:MSRC MSRC
such that, for each <m,s,r,c>MSRC, if p starting from the state <m,s,r,c> terminates in a state <m',s',r',c'> then
run[p](<m,s,r,c>) = <m',s',r',c'>
and otherwise (i.e., if there is no termination) run[p](<m,s,r,c>) is undefined.
end

Definition: The {<id>, <be>, <ae>, <st>}-ary mapping RUN*:U(STP)U(SEM) is defined as follows:

DefineRUN*_<id>to be the identity on Id

Given pSEM_<be>(= ProgS) define

RUN*_<be>(p):MM{true, false}
< m, top(s')'> if run[p](m, , 0, 0) = <m',s',r',c'> with top(s'){true. false} and m'Stt
undefined otherwise

Given pSEM_<ae>(= ProgS) define

RUN*_<ae>(p):MMZ
< m, top(s')'> if run[p](m, , 0, 0) = <m',s',r',c'> with top(s')Z and m'Stt
undefined otherwise

Given pSEM_<st>(= ProgS) define

RUN*_<be>(p):MM
m' if run[p](m, , 0, 0) = <m',s',r',c'> with m'Stt
undefined otherwise

end

Theorem: The restriction, RUN, of RUN* to CMP is a homomorphism from CMP to SEM.

Proof:
Click here for the details.
end

Click here to see a JavaScript implementation of the homomorphic compiler for LANG1 into StackM