A Grammar for a Structured Programming Language,
LANG1
In this chapter we begin the application of the concepts of the previous
chapters to a detailed example -- a simple structured programming language
called LANG1. In this section we present the syntax
of LANG1. In subsequent chapters we will explore its semantics,
the parsing of LANG1 programs, and the compiling of LANG1
onto a simple stack machine. The aim is to show that the syntax,
semantics and compilation are all given by initial homomorphisms from an
initial algebra corresponding to the abstract syntax of LANG1.
It is well-known that most programming languages do not have context-free
grammars. LANG1 has the rather unusual property that it has
a context-free grammar that generates all, and only, correct LANG1
programs. It is this fact that makes it possible to describe
the syntax, semantics and compilation of LANG1 in such an algebraic
manner. Lest this suggest that this example is not of "real computer
science interest", we note that in later parts of this e-book we will show
how these algebraic ideas can be applied to languages that do not have
such nice context-free grammars.
Here is the context-free grammar for LANG1:
N = {< id>,<be>,<ae>, <st>}
T = standard keyboard symbols (including space)
P consists of the following productions
a
<id>::= a
b
<id>::=b


z
<id>::= z
-2,147,483,648 <ae>::=
-2,147,483,648


-1
<ae>::=-1
0
<ae>::= 0
1
<ae>::= 1


2,147,483,647 <ae>::=
-2,147,483,647
tr
<be>::=true
fa
<be>::=false>
not
<be>::= ~<be>
and
<be>::=(<be>&<be>)
eq
<be>::= (<ae>==<ae>)
leq
<be>::=(<ae><=<ae>)
id2ae
<ae>::=<id>
succ
<ae>::=succ(<ae>)
pred
<ae>::=pred(<ae>)
neg
<ae>::=(-<ae>)
add
<ae>::=(<ae>+<ae>)
mult
<ae>::=(<ae>*<ae>)
assign
<st>::=<id>:=<ae>
compos
<st>::=<st>;<st>
if
<st>::=If<be>then<st>else<st>fi
wdo
<st>::=While<be>do<st>od
S = <st>
Note: While the above grammar
looks reasonably concise, it really isn't. The ellipses (" ")
disguise the fact that there are actually 4,294,967,288 productions.
")
disguise the fact that there are actually 4,294,967,288 productions.
"Proposition" L(G) is precisely the
set of all well-formed LANG1 programs.
The signature corresponding to the grammar for LANG1 is
The Signature LANG1syn in mathematical
form:
name: LANG1syn
sorts: {<id>, <be>, <ae>, <st>}
operators:
LANG1syn(<id>) = {LANG1var}
LANG1syn(<be>) = {tr, fa}
LANG1syn(<ae>) = {LANG1Int}
LANG1syn(<be>, <be>) = {not}
LANG1syn(<be>.<be>,<be>) = {and}
LANG1syn(<ae>.<ae>,<be>) = {eq,
leq}
LANG1syn(<ae>,<ae>) = {succ, pred}
LANG1syn(<id>,<ae>) = {id2ae}
LANG1syn(<ae>.<ae>,<ae>) = {add,
mult}
LANG1syn(<id>.<ae>,<st>) = {assign}
LANG1syn(<st>.<st>,<st>) = {compos}
LANG1syn(<be>.<st>.<st>,<st>)
= {if}
LANG1syn(<be>.<st>,<st>) = {wdo}
End of signature LANG1syn.
where LANG1var is the characteristic
function of the set {'a', 'b', ...,'z'} and LANG1Int
is the characteristic function of the set of all JavaScript integers.
We can, of course, also present the grammar in "programming form"
The Signature LANG1syn in programming form:
name: LANG1syn
sorts: {<id>, <be>, <ae>, <st>}
operators:
LANG1var: --><id>
tr: --><be>
fa: --><be>
LANG1Int: --><ae>
not:<be>--> <be>
and:<be>.<be>--><be>
eq:<ae>.<ae>--><be>
leq:<ae>.<ae>--><be>
succ:<ae>--><ae>
pred:<ae>--><ae>
id2ae:<id>--><ae>
add:<ae>.<ae>--><ae>
mult:<ae>.<ae>--><ae>
assign:<id>.<ae>--><st>
compos:<st>.<st>--><st>
if:<be>.<st>.<st>--><st>
wdo:<be>.<st>--><st>
End of signature LANG1syn.
And, finally, here is the spaghetti and meatball diagaram for the signature.
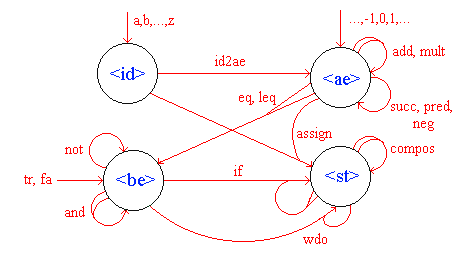
Any expression written in the signature LANG1syn
corresponds directly to the abstract syntax of an expression generated
by the context-free grammar of LANG1. The correspondence between
the abstract and the concrete syntax is given by the unique homomorphism
from the initial algebra generated by LANG1syn
and an appropriate LANG1syn-algebra of strings,
alg_LANG1Conc ("Conc" as in "Concrete")
which is given below. Thus, given a LANG1syn-expression
such as
"compos(assign(b( ), 1( )), wdo(leq(1(
), id2ae(a( ))), compos(assign(b( ), mult(id2ae(a( )), id2ae(b( )))), assign(a(
), pred(id2ae(a( )))))))"
we can use the homomorphism function, aitch, with first argument
"alg_LANG1Conc", to produce the string corresponding to its concrete syntax:
b:=1 ; While (1 <= a) do b:=(a * b)
; a:=(a-1) od
Note, This computation is not instantaneous
-- e.g., it took one to two seconds on 200 MH PC employing
Netscape 4.62.
The algebra alg_LANG1Conc
The signature of alg_LANG1Conc is: LANG1syn
The carriers of alg_LANG1Conc are: Not
Specified
The operations of the algebra alg_LANG1Conc are:
[LANG1Var, poop]
["tr", "true"]
["fa", "false"]
["not", "'~'+arg[1]"]
["and", "'('+arg[1]+' & '+arg[2]+')'"]
["eq", "'('+arg[1]+' == '+arg[2]+')'"]
["leq", "'('+arg[1]+' <= '+arg[2]+')'"]
[numQ, str2num]
["id2ae", "''+arg[1]"]
["neg", "'(-'+arg[1]+')'"]
["succ", "'('+arg[1]+'+1)'"]
["pred", "'('+arg[1]+'-1)'"]
["add", "'('+arg[1]+' + '+arg[2]+')'"]
["mult", "'('+arg[1]+' * '+arg[2]+')'"]
["assign", "''+arg[1]+':='+arg[2]"]
["compos", "''+arg[1]+' ; '+arg[2]"]
["if", "'If '+arg[1]+' then '+arg[2]+'
else '+arg[3]+' fi '"]
["wdo", "'While '+arg[1]+' do '+arg[2]+'
od'"]
End of algebra alg_LANG1Conc
