Context-Free Grammars
In this section we will review some "well-known" results about the relationship
between context-free grammars and algebras. These results underly
the algebraic approach to the semantics of programming languages.
It is "well-known" that every context-free grammar, G,
-
corresponds to a many sorted signature,
 (G),
with a sort for each non-terminal and an operator for each production in
G,
(G),
with a sort for each non-terminal and an operator for each production in
G,
-
that the free algebra for
 (G)
corresponds to the abstract syntax of G
(G)
corresponds to the abstract syntax of G
-
that the concrete syntax is a
 (G)-algebra..
(G)-algebra..
We will show how the programs given in the section Signatures,
Algebras and Homomorphisms can be used to explore these results.
Outline:
Context-free grammars where originally developed by Noam Chomsky
as a means for describing the underlying syntax (grammar) of natural languages.
It was first used in computer science to describe the grammar of the programming
language ALGOL 60. For a while computer scientists used the term
"ALGOL-like languages" rather than Chomsky's term, "context-free language".
However it was eventually realized that ALGOL60 was actually not an "ALGOL-like
language" and so the term "ALGOL-like-language" ceased to be used.
We will later give an example of a programming language, the language LANG1,
that does have a context-free grammar. However, most programming
languages (and all natural languages) do not have context-free grammars.
Despite this fact, context-free grammars are still very useful and
reflect the underlying algebraic structure of both kinds of languages.
Later we will look further into the question of the relationship between
the syntax of programming languages and context-free grammars.
Definition:
A context-free grammar G consists of
-
T, a set (of terminal symbols)
-
N, a set (of non-terminal symbols)
where N
 T =
T =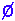 .
.
-
P
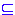 Nx(N
Nx(N T)* (a set of productions)
T)* (a set of productions)
-
S
 N (the start symbol)
N (the start symbol)
We can write a production as a pair p
= <A0, a0A1a1...Anan>
where 0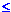 n,
each Ai
n,
each Ai N,
and each ai
N,
and each ai T*.
Sometimes a production is written in the form
p A0
T*.
Sometimes a production is written in the form
p A0  a0A1a1...Anan
a0A1a1...Anan
A context-free grammar G
= <T, N, P, S> defines a subset L(G)
of T* calledthe
context free language generated by G.
The set L(G)
is defined using the relation  G:(N
G:(N T)*
T)*  (N
(N T)* where w
T)* where w Gu
iff there exists a production p = <L,R>
Gu
iff there exists a production p = <L,R>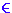 P
and a,b
P
and a,b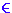 (N
(N T)* such that w=aLb
and u = aRb.
T)* such that w=aLb
and u = aRb.
Let  G
be the transitive closure of
G
be the transitive closure of  G.
Then L(G) is defined to be
{ u
G.
Then L(G) is defined to be
{ u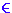 T* | S
T* | S G
u }.
G
u }.
end
Examples:
Example: Let the grammar G
be such that T = {0, 1}, let N
= {A}, let P = {<A, 0>,
<A, 1A1>}, and let A
also be the start symbol. Then L(G) =
{0, 101, 11011, ... 1n01n...}
end
Example: Logical Expressions:
-
T = {true, false, and, or, not, (, ) },
-
N = {E},
-
P = {<E, true>, <E, false>, <E, (E and E)>,
<E, (E or E)>, <E, not(E) > },
-
and the start symbol is E.
The resulting context-free language, L(G), will be the set of all well-formed
logical expressions without variables. Examples of elements of L(G)
include
-
true
-
(true or false)
-
(true and (false or not(false)))
end.
Example: Arithmetic Expressions
I:
-
T = { 0,1,2,3,4,5,6,7,8,9,+,*,-,/,(,) }
-
N = { Digit, Pint, Int, Exp }
-
P = { <Digit, 0>, <Digit, 1>, <Digit, 2>, <Digit,
3>, <Digit, 4>, <Digit, 5>, <Digit, 6>, <Digit, 7>, <Digit,
8>, <Digit, 9>,
<PInt, 1>, <PInt, 2>, <PInt, 3>, <PInt, 4>, <PInt, 5>, <PInt,
6>, <PInt, 7>, <PInt, 8>, <PInt, 9>, <PInt, PInt.Digit>,
<Int, PInt>, <Int, 0>, <Int, -PInt>,
<Exp, Int>, <Exp, (Exp + Exp)>,<Exp, (Exp * Exp)>,<Exp,
(Exp - Exp)>,<Exp, (Exp / Exp)>}
end.
Example: A simple sub-grammar of English.--
yet to come
Example: LANG1 -- click
here to see the context-free grammar of a simple programming language.
end.
The Signature of a Context-free Language
Given a context-free grammar G = <T, N, P, S>
define Sig(G), the signature of G,
to be the signature with
-
a sort n for each nonterminal n
 N.
N.
-
an operator for each production in P
Specifically, if p = <A0,
a0A1a1...Anan>
is a production in P then the corresponding
operator is p:A1x...x.An A0.
A0.
Example: Let the grammar G
be such that T = {0, 1}, let N
= {A}, let P = {<A, 0>,
<A, 1A1>}, and let A
also be the start symbol. Then the corresponding signature, Gram1,
is:
The Signature Gram1 in mathematical form:
name: Gram1
sorts: {A}
operators:
Gram1(A) = {p0}
Gram1(A,A) = {p1}
End of signature Gram1.
Note that, with this signature the only Gram1-terms
that we can generate are of the form p1n(p0(
)) (where p10(p0(
)) = p0( ) and p1n+1(p0(
)) = p1( p1n(p0(
))) ).
end.
Example:
To see the signature corresponding to the example of a context-free
grammar for arithmetic expressions click here.
end.
The Algebras of a context-free Grammar
Information is lost in the process of going from a grammar to its signature
-- that is, you can not reconstruct the complete grammar from the signature
because the operators lack the strings of terminal symbols found in the
productions and the signature does not contain any information about the
start symbol. The missing information given by the strings of terminal
symbols corresponds to a Sig(G)-algebra, the
choice of the start symbol is just the designation of one of its sorts.
The grammar-as-a-whole then corresponds to the unique homomorphism hG:TSig(G) Alg(G) from the initial Sig(G)-algebra
to the algebra Alg(G). Our claim
is that, if s
Alg(G) from the initial Sig(G)-algebra
to the algebra Alg(G). Our claim
is that, if s S
is
the start symbol for G then the image of (TSig(G))s
under the homomorphism
hG is exactly
the set,
L(G), i.e., the context free language
generated by G.
S
is
the start symbol for G then the image of (TSig(G))s
under the homomorphism
hG is exactly
the set,
L(G), i.e., the context free language
generated by G.
In terms more familiar to computer scientists, a Sig(G)-term,
t,
is the abstract syntax of the string hG
(t)
which, in turn, is a concrete syntax for t.
If there are two terms t,t'  (TSig(G))s
such that t
(TSig(G))s
such that t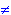 t but hG
(t)
= hG
(t') then we say
that the grammar G is ambiguous.
t but hG
(t)
= hG
(t') then we say
that the grammar G is ambiguous.
Since the real interest is in the image of (TSig(G))s
under the of hG , we have some
freedom in the definition of Alg(G):
-
there is no harm in adding "extraneous elements" to the carriers of Alg(G).
Indeed
there is real benefit if the "extraneous elements" simplify the presentation
of the algebra.
-
it doesn't matter what the operations do when the "extraneous elements"
appear as arguments
This being the case we can give the following definition for Alg(G)
-
For each n
 N
let Alg(G)n = T*,
the set of all strings on the set T of terminal
symbols from G.
N
let Alg(G)n = T*,
the set of all strings on the set T of terminal
symbols from G.
-
For each p
 P,
if p = <A0, a0A1a1...Anan>,
then let pAlg(G):(T*)n
P,
if p = <A0, a0A1a1...Anan>,
then let pAlg(G):(T*)n  T* such that, for all <t1,...,tn>
T* such that, for all <t1,...,tn>  (T*)n
, we have pAlg(G)
(t1,...,tn )
= a0t1a1...tnan
the concatenation of the strings in the indicated order.
(T*)n
, we have pAlg(G)
(t1,...,tn )
= a0t1a1...tnan
the concatenation of the strings in the indicated order.
This definition for pAlg(G)
can be directly translated into a JavaScript expression suitable
for use with our JavaScript representation of algebras as
pAlg(G) (t1,...,tn)
= a0 + arg[0] + a1 + ...+ arg[n] + an
.
Example: Let the grammar G
be such that T = {0, 1}, let N
= {A}, let P = {<A, 0>,
<A, 1A1>}, and let A
also be the start symbol. Then the corresponding algebra, alg_Gram1,
is the G-algebra with
-
carrier {0, 1}*
-
operations
p0alg_Gram1:  {0,
1}*, p0alg_Gram1 (
) = 0
{0,
1}*, p0alg_Gram1 (
) = 0
p1alg_Gram1: {0,1}*  {0,
1}*, p1alg_Gram1 (
t ) = 1t1
{0,
1}*, p1alg_Gram1 (
t ) = 1t1
The corresponding algebra in JavaScript is given
by alg_Gram1
The algebra alg_Gram1
The signature of alg_Gram1 is: alg_Gram1
The carrier of alg_Gram1 is the set , {1, 0}*
. of all strings of zeros and ones. (but is not actually specified in the
UA-Calculator version).
The operations of the algebra alg_Gram1 are:
["p0", "'0'"]
["p1", "'1'+arg[1]+'1'"]
End of algebra alg_Gram1
end
![]() G:(N
G:(N![]() T)*
T)* ![]() (N
(N![]() T)* where w
T)* where w![]() Gu
iff there exists a production p = <L,R>
Gu
iff there exists a production p = <L,R>![]() P
and a,b
P
and a,b![]() (N
(N![]() T)* such that w=aLb
and u = aRb.
T)* such that w=aLb
and u = aRb.
![]() G
be the transitive closure of
G
be the transitive closure of ![]() G.
Then L(G) is defined to be
{ u
G.
Then L(G) is defined to be
{ u![]() T* | S
T* | S![]() G
u }.
G
u }.
![]() (TSig(G))s
such that t
(TSig(G))s
such that t![]() t but hG
(t)
= hG
(t') then we say
that the grammar G is ambiguous.
t but hG
(t)
= hG
(t') then we say
that the grammar G is ambiguous.
![]() {0,
1}*, p1alg_Gram1 (
t ) = 1t1
{0,
1}*, p1alg_Gram1 (
t ) = 1t1