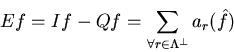 |
(1) |
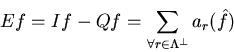 |
(1) |
Where ar(f) are the Fourier coefficients of the integrand
and
![]() is the reciprocal lattice.
Since the Fourier coefficients decay rapidly for large
is the reciprocal lattice.
Since the Fourier coefficients decay rapidly for large
![]() for natural periodic integrands,
we seek lattice rules, Q, for which
for natural periodic integrands,
we seek lattice rules, Q, for which
![]() has as few points as possible for small
has as few points as possible for small
![]() .
.
To attain high degree, d, we seek lattices
![]() with elements as
far from the origin as possible. The 1-norm of the point closest to the origin,
with elements as
far from the origin as possible. The 1-norm of the point closest to the origin,
![]() ,
defines the trigonometric degree, d, as
,
defines the trigonometric degree, d, as
![]() .
.
A cubature rule need not only be accurate, a good rule is also economical.
A convenient measure of the cost of the rule is N(Q), the number of
function evaluation
needed to carry out the calculation.
This depends directly on the density of the points in the lattice
![]() .
.
An optimal rule of degree, d, is optimal if its abscissas count is less or equal to the abscissa count of any other rule of degree d. Optimal rules are known for all degrees in dimension 1 and 2. For higher dimension optimal rules are only known for the degree 0,1,2 and 3. All these rules are known to be lattice rules, thus it is reasonable to restrict the search for rules of optimal trigonometric degree to lattice rules.
Ronald Cools and James Lyness have recently conducted a computer search for
good lattice rules in dimension 3 and 4.
They define a class of lattices
![]() and restrict their search
to either this class, or well defined subclass of this.
There are good reasons to believe that
any optimal lattice rule belongs to class
and restrict their search
to either this class, or well defined subclass of this.
There are good reasons to believe that
any optimal lattice rule belongs to class
![]() ,
but this has not been proved.
The optimal rule within this class is called K-optimal.
,
but this has not been proved.
The optimal rule within this class is called K-optimal.
A member of
![]() is characterized by having generating vectors
on s different facets of the s-dim octahedron.
is characterized by having generating vectors
on s different facets of the s-dim octahedron.
Our previous search has only covered one equivalence class. Now the program is modified so it might cover all 11. An input parameter decides whether the search should be over all equivalence classes or only the basic equivalence class.
Even when restricted to only one equivalence class, the search become exhaustive
for large
![]() .
A further restriction is then applied. By symmetry argument one might hope
it is sufficient to consider only a generator vector a
at the first facet in which the size of the
coordinates are ordered. This will reduce the number of candidate lattices
asymptoticly to M(s,
.
A further restriction is then applied. By symmetry argument one might hope
it is sufficient to consider only a generator vector a
at the first facet in which the size of the
coordinates are ordered. This will reduce the number of candidate lattices
asymptoticly to M(s,![]() )/2s.
We name this restriction, searching only the
small triangle. It is necessary to point out that the small triangle
search misses out on some lattices in the corresponding equivalence class
and thus no guaranty the K-optimal rule
of the associated equivalence class is found anymore.
)/2s.
We name this restriction, searching only the
small triangle. It is necessary to point out that the small triangle
search misses out on some lattices in the corresponding equivalence class
and thus no guaranty the K-optimal rule
of the associated equivalence class is found anymore.
Corresponding to the different savings discussed above we have now modified the code to permit us to set the search space to any of the 3 modes:
1. Full search over all equivalence classes.
2. Full search over the basic equivalence class only.
3. Restricted search over small triangle, only basic equivalence class.
Technical details on how the search is carried out can be found here and instruction on how to participate is here.
We've also written a white paper on our previous search available here.