Fasta is a heuristic method for local sequence alignment and has many similarities to the BLAST method. When aligning a query sequence q against a database sequence d it first identifies local ungapped alignments (diagonal hits). These can be combined by constructing a graph describing the hits and the relations between these. For each local ungapped alignment, a node is made. There is a directed edge from one node to another if the alignment corresponding to the first node ends before the second starts - in both sequences. This means that the two local alignments could be part of the same alignment. Each node is given a weight reflecting the goodness of the corresponding local alignment. The edges are weighted according to the distance between the local alignments (along each of the sequences).
Example: In the upper figure, the local alignments are shown in a matrix where the first sequence runs along the vertical axis and the second runs along the horisontal axis (the matrix corresponds to a dynamic programmming matrix that could be used for local or global alignment of the two sequences).
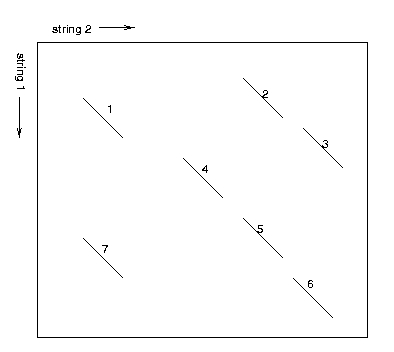
The figure below shows a graph representation of the local alignments above. The nodes are numbered according to the numbers in the figure above. Node weights are given as red numbers and edge weights are edge weights.
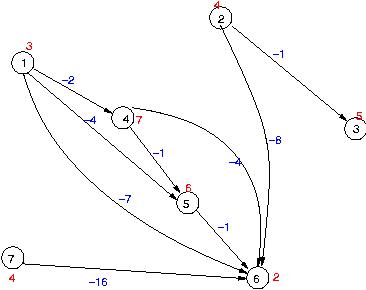
Task: Try using depth-first-search (DFS) and breadth-first-search (BFS) in order to find the heaviest path in the graph (the weight of a path is the sum of node and edge weights along the path).
We have looked at methods for comparing pairs of strings. One approach allowing to compare more than two strings, is to search for patterns that are shared by the strings. Patterns could for example be regular expressions. The simples type of patterns that are frequently used is the so-called substring patterns. A string S matches a pattern P if it contains P as a substring. For instance, ACGTAGTA matches the pattern GTAG, but not the pattern CC. We can formulate a problem of finding the longest substring (substrings) shared by a given set of strings as a search problem. The root in the search tree represents the empty string e. A node in the search tree that represents the string p has a child node that represent the string px for each letter x in the alphabet. This means that a node on level r (r levels down from the root) represents a string with r letters, and if the alphabet has t letters, then each node will have t children nodes. For each node, we can match the corresponding pattern against all the strings. If not all strings match the pattern p, we do not need to explore extensions of p. What does it mean for the search? We are given the strings ACGTT, TACGTA, GCACGT, and TTACGTAA. Show the search tree allowing us to find the longest substring shared by all strings. (We are using the alphabet {A,C,G,T}.) Can you think of arguments for using DFS rather than BFS (or vice versa) for exploring the tree?
The problem of calculating the edit distance between two strings is to find the minimum number of operations that are required in order to change one string into the other where the operations are substitution, insertion, and deletion (single letter). This can be formulated as a graph problem, where the edit distance corresponds to the shortest path from the start node S to the goal node Gin a weighted graph, the edit graph. Draw the edit graph for the strings AC and AT.
- The dynamic programming principle according to Winston can now be applied to the search for the shortest path in the edit graph. Discuss how this is similar to the standard dynamic programming algorithm for sequence alignment.
- Can the A* algorithm be used to find the edit distance? If so, would it be faster than the standard dynamic programming algorithm to calculate the edit distance between two strings? (Refer to http://www.ii.uib.no/~inge/i181v2000/Winston-sok.html.)
-
If we use similarity scoring instead of distance, the problem becomes
finding the longest path in the graph. How will this affect
the search problem, especially the A* algorithm?