SAGA - Scientific Computing with Algebraic and Generative Abstractions

Coordinate-Free Numerics

Coordinate-free numerics is the use of coordinate-free mathematical abstractions in the numerical solution of problems, typically partial differential equations. It turns out that the coordinate-free formulations are much better software artefacts than the standard approaches in numerical and applied mathematics. Coordinate-free software is more modular and more adaptable to changes in problem requirements. The approach has been shown to be robust (meaning only small, contained parts of the code needs to be modified) for changes in coordinate system (obviously), changes in numerical methods (FDM and FVM), changes in the partial differential equations themselves (e.g., from elastic to poro-elastic wave equation), and parallelisation of code.

The Sophus software library

Sophus is a software library carefully designed to mimic the abstract structure of the mathematics of partial differential equations, as used in the discription of many natural and industrial phenomena. Its apparatus supports coordinate free numerics in the formulation and development of solvers to problems. By requiring strict adherence to specified interfaces, we have been able to achieve that different implementations of the same mathematical concepts are basically interchangeable. The Sophus library components can be presented through different layers of abstractions. The interchangeability of modules within a layer allows software developers to experiment with different solution strategies and HPC architectures without the need for extensive reprogramming. For example, the change from a sequential to a parallel version of a seismic simulator does not involve any reprogramming of the rest of the solver application. Currently the Sophus library is implemented using C++.

Experience using SAGA methodologies compared to traditional methodologies

 The main industrial relevance of SAGA is the investigation and promotion of more effective development techniques for problem specific modelling. The increase in modelling productivity is expected to come from improved program structure, which should result in smaller source code and more self-contained sections of the code, thus significantly reducing the size of the code that has to be modified when a (slightly) different model is needed. Software costs typically increase much more than linearly in code size due to longer development times and higher maintenance costs.

To exemplify the differences between SAGA software methodologies and traditional software methodologies we will briefly present a computational fluid dynamics case study. This involved developing a solver for a coating problem in axio-symmetric form, with the use of the finite element method (FEM) as numerical discretisation technique. The case study revealed a cultural gap between the traditional thinking, where everything is made explicit when approaching a computational modelling problem, and the thinking needed for a more algebraic approach, where the focus is on the abstract mathematical level. This mathematical level is directly supported by the Sophus library abstractions.

Traditional development of solver

Traditionally development of a computational model starts by looking at the main ideas of the mathematical solution of the problem, glossing over details that are technically involved but contribute little to the understanding of the problem. For simplicity, a Cartesian coordinate system is used for this part. Then the development focuses on the discretisation technique, in this case the FEM, and makes a simplified overview of the underlying mathematics of the technique. Further development of the solver is now closely linked to its realisation using the FEM technique. Technical details are then added at the discrete level, but still within the framework of the Cartesian coordinate system. As the study approaches the end, it is expanded with various material such as the use of axio-symmetric coordinate system, which has a marked influence on the way the operators are defined, or semi-implicit time stepping to increase stability and convergence. These pieces are studied independently of each other, where important details, such as how to do the integration of the scalar fields, are not looked upon in depth. The implementor of the solver now has to redo the development, tracing the added features through the discretised presentation, finally ending with a concrete level algorithm that takes all the presented information into account.

This development strategy can be summarised in the figure below, where we see that parallelisation of the code involves further modification of the whole system.

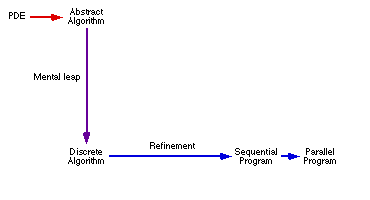
Traditional development strategy

The upper level represents reasoning at the coordinate free, continuous mathematics level. This level is abandoned as soon as the solver strategy has been formulated. The mental gap occurs when taking into account coordinate systems and discretisations. All further refinement now takes place on the concrete level, using machine oriented primitives directly.

SAGA oriented development of solver

Using the SAGA methodologies the development of the solver is taken as far as possible on the abstract level. This means that integration schemes for variational formulations have to be discussed quite early, and modifications of the strategy due to semi-implicit time-stepping will be handled at a coordinate free level.

Choice of coordinate systems involves selection of the appropriate tensor module from the library. If an axio-symmetric version is not present it will have to be developed. This development is independent of the rest of the solver, and a new tensor module typically involves 1000-5000 lines of code.

The introduction of discretisation technique is again an orthogonal issue. If an FEM implementation is not part of the library, an independent development of such a module has to take place. A new discretisation technique typically involves a library module containing 1000-5000 lines of code.

This development strategy can be summarised in the figure below, where we see that parallelisation of the solver is also a matter of choice of library modules.

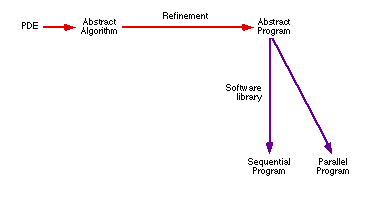
Algebraic development strategy

Here the development at the abstract level also includes writing the program code. This is possible since we match the mathematical concepts with software abstractions from the Sophus library. The library modules then bridge the gap down to the machine level. If a desired module is missing from the library, it is developed and coded independently of the rest of the solver application.

Comparing the development methodologies

Comparing traditional numerical software development with the SAGA software methodology we see that the former requires us to be involved in the whole code for the system. This may be as much as 20000 lines, representing a large intellectual effort in itself. Developers knowledgeable in the area will normally have access to library routines, but often these will have to revisited when a new solver application is developed.

The SAGA approach focuses on the abstract mathematical development, and a solver at this level typically remains at 2000 lines of code, even when all technical details are exposed.

We may summarise this difference in the following diagram.

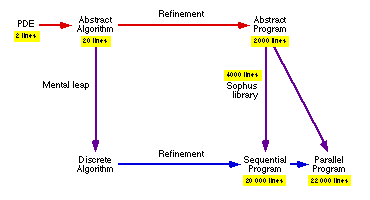
Contrasting development strategies

The lines of code have been added to indicate the size of the code one needs to worry about at different key stages. We have also included the cost of writing a missing library module in the transition to a working program on the right.

We see here that the amount of code one needs to be concerned with during a development process may decrease to about a tenth of the traditional code size when using algebraic software methodologies. This represents a tremendous saving in software development costs, and a dramatic increase in flexibility to test out new solver schemes. Crucial to this improvement is the use of a library of interchangeable software modules carefully tuned to match the abstract mathematical concepts. The abstractions also allow switching between sequential and parallel HPC versions of the solver without the need for reanalysing or rewriting the software.

These pages last updated June 2005 ©2005 Magne Haveraaen, University of Bergen, Norway.
SAGA contact address.
Main SAGA WWW page.