Parallel Execution of Recurrences: Linear Array
This shows how
efficient prototyping of recurrences
also can utilise the processing power of parallel machines.
Static View of Linear Array
A linear array is a computer where the processing elements are connected
in a linear fashion, i.e., each node is connected to two other nodes,
except the two end nodes which are connected to just one neighbour. The
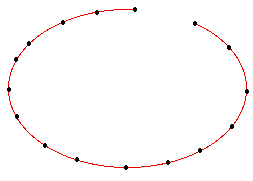
figure shows a 16 node linear array connected computer
Space-Time View of Linear Array
If we try to imagine how the communications of a linear array may appear
if we draw them schematically in time, we may get the following figure.
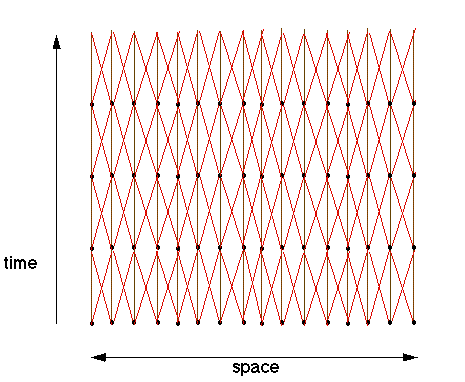
Here all the processors of the linear array are depicted at every time-step,
as if all computations where taking place instantaneously and synchronously.
The communications now go between the timesteps, to the neighbours as
defined by the static configuration of the linear array. These lines
are marked with red, diagonal lines forward in time. In addition, a processor may
retain information between computation steps. This is depicted as
a communication from a processor to itself (brown vertical lines).
Heatflow Problem Embedded in Linear Array
The one-dimensional heatflow computation
may easily be embedded in the linear arrays computation structure.
The dependencies of this computation exhibits the same graph as the
communications of the linear array. An
animated demo
of this has been prepared as Java code.
Butterfly Embedded in Linear Array
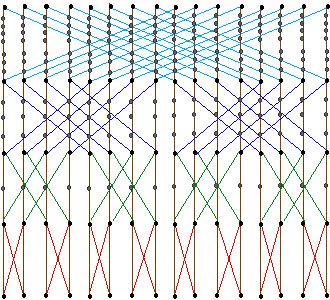
Butterfly computations can also be embedded
in the linear array.
This requires us to use more than one time-step for communications,
and progressively more timesteps as the communications of the butterfly
grow longer. This can be seen in the figure below, which shows a height
4 butterfly embedded in a 16 node linear array using 16 timesteps.
The scale is logarithmic in the time-direction, and the processors
have been shaded in grey when they do not compute but just forward
communications.
The parallelisation technique
The embedding of a computation in a parallel machine over time
- maps computations to processors at specific time-steps,
- maps dependencies to paths in the parallel machine's space-time
communication structure.
The mapping is user definable and expressible as program code. This gives
the programmer full control over the computation, but still avoids lots
of detail in the writing of parallel programs.
This shows some of the potential efficient
prototyping of recurrences
has for defining parallel programs.
© 1997 Magne Haveraaen, University of Bergen, Norway.



